Cara menghitung volume tabung perlu dipahami dalam pembelajaran tentang bangun ruang. Tabung adalah bangun ruang tiga dimensi yang terdiri dari dua lingkaran dengan ukuran yang sama sebagai tutup dan alasnya, yang dihubungkan oleh permukaan melingkar.

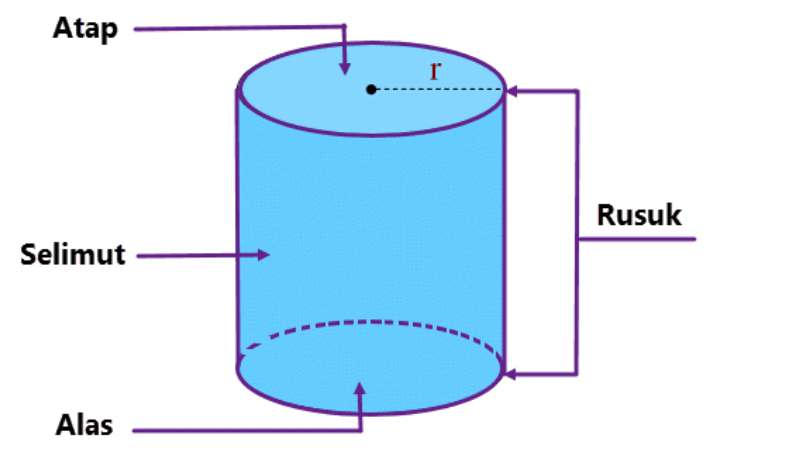
Ciri-ciri tabung termasuk tidak memiliki titik sudut, rusuk, atau bidang diagonal. Sisi tabung terdiri dari dua lingkaran (tutup dan alas) serta satu permukaan melingkar. Tinggi tabung diukur dari jarak antara pusat lingkaran alas dan lingkaran atas.

Untuk menghitung volume tabung, gunakan rumus berikut: V = π x r² x t, di mana:

• V adalah volume.
• π adalah nilai pi, sekitar 3.14.
• r adalah jari-jari.
• t adalah tinggi.

Dalam komponen tabung, terdapat dua lingkaran sejajar yang membentuk tutup dan alas, dengan permukaan melingkar yang menghubungkannya. Lingkaran alas memiliki jari-jari (r) dan diameter (d) yang sama, di mana jari-jari adalah jarak dari pusat lingkaran ke tepinya, dan diameter adalah dua kali jari-jari. Tinggi (h) adalah jarak vertikal antara kedua lingkaran.

Bentuk tabung adalah salah satu bentuk geometri dasar dalam matematika dan geometri. Tabung adalah sebuah benda tiga dimensi yang terdiri dari dua bagian utama: dua lingkaran yang berdekatan pada ujung-ujungnya dan permukaan melengkung yang menghubungkan kedua lingkaran tersebut. Bentuk tabung ini seperti tabung dalam kehidupan sehari-hari, seperti botol minuman atau gulungan kertas toilet. Tabung memiliki beberapa karakteristik penting:

1. Lingkaran Dasar: Tabung memiliki dua lingkaran, satu di bagian atas dan satu di bagian bawah, yang sering disebut sebagai lingkaran dasar. Lingkaran ini memiliki jari-jari yang sama.
2. Tinggi: Tinggi tabung adalah jarak antara dua lingkaran dasar. Ini adalah garis lurus yang menghubungkan pusat lingkaran atas dan bawah.
3. Permukaan Samping: Permukaan samping tabung adalah permukaan melengkung yang mengelilingi ruang di antara dua lingkaran dasar. Permukaan samping tabung ini biasanya berbentuk silinder.

Baca Juga : Soal Latihan ASPD Sekolah Dasar 2023 -IPA

Ciri-ciri umum tabung meliputi:

• Memiliki dua alas berbentuk lingkaran.
• Tidak memiliki titik sudut.
• Tidak memiliki rusuk.
• Tidak memiliki bidang diagonal.
• Memiliki tinggi tabung.

Contoh-contoh soal menghitung volume tabung:

1. Volume tabung dengan r = 5 cm dan t = 10 cm adalah 785 cm³.
2. Volume tabung dengan r = 10 cm dan t = 20 cm adalah 6280 cm³.
3. Volume tabung dengan r = 6 cm dan t = 7 cm adalah 792 cm³.
4. Volume tabung dengan r = 10 cm dan t = 30 cm adalah 9420 cm³.
5. Volume tabung dengan d = 20 cm dan t = 10 cm adalah 3140 cm³.

Contoh Soal dan Penyelesaian

Contoh Soal 1: Sebuah wadah berbentuk tabung memiliki tinggi 10 cm dan jari-jari lingkaran dasarnya adalah 4 cm. Hitunglah volume wadah tersebut.

Penyelesaian: Volume tabung dapat dihitung dengan rumus berikut:

V=π×r²×h

Di mana:

• V adalah volume tabung,
• π (pi) adalah konstanta matematika, dengan perkiraan 3,14,
• r adalah jari-jari lingkaran dasar tabung, dan
• ℎh adalah tinggi tabung.

Mari kita substitusi nilai-nilai yang telah diberikan ke dalam rumus:

• V=3.14×(4 cm)2×10 cm
• V=3.14×(4cm)2×10cm
• V=3.14×16 cm2×10 cm
• V=3.14×16cm²×10cm

Sekarang, kita dapat menghitung volume:

• V=3.14×160 cm³
• V=3.14×160cm³
• V=502.4 cm³
• V=502.4cm³

Jadi, volume wadah tabung tersebut adalah 502.4 cm kubik atau cm³.

Contoh Soal2: Sebuah tabung memiliki jari-jari lingkaran dasar sebesar 5 cm dan tinggi 10 cm. Hitunglah volume tabung tersebut.

Penyelesaian:

Untuk menghitung volume tabung, kita dapat menggunakan rumus:

Volume = Luas Lingkaran Dasar × Tinggi

Langkah 1: Hitung Luas Lingkaran Dasar Rumus luas lingkaran adalah:

Luas = π × r²

Di mana π (pi) adalah konstanta yang sekitar 3,14, dan r adalah jari-jari lingkaran dasar.

• Jadi, Luas Lingkaran Dasar = π × (5 cm)²
• Luas Lingkaran Dasar = 3.14 × 25 cm²
• Luas Lingkaran Dasar = 78.5 cm²

Langkah 2: Hitung Volume Sekarang, kita bisa menggantikan nilai luas lingkaran dasar dan tinggi ke dalam rumus volume:

Volume = 78.5 cm² × 10 cm Volume = 785 cm³

Jadi, volume tabung tersebut adalah 785 cm³

Itu adalah cara menghitung volume tabung. Pastikan untuk memahami rumus-rumus yang digunakan dan menggantikan nilai-nilai yang diberikan dalam soal ke dalam rumus untuk mendapatkan jawaban yang benar.

Tabung dapat digunakan dalam berbagai konteks, termasuk matematika, fisika, dan teknik. Di matematika, tabung adalah salah satu bentuk geometri yang sering digunakan dalam perhitungan volume dan luas permukaan. Dalam dunia nyata, banyak objek seperti tabung, seperti tabung hidrolik, tangki penyimpanan, dan berbagai jenis wadah, yang memiliki bentuk serupa.